BECE Maths 2018 Past Questions & Answers – Papers 2 & 1

JUNE 2018
MATHEMATICS 2

PAPER 2
ESSAY
1 hour

Answer four questions only.
All questions carry equal marks.
All working must be clearly shown.
Marks will not be awarded for correct answers without corresponding working

1. (a) Solve the inequality and represent the answer on the number line.

(b) Given that  find 2t + k

(c) The sides of a triangle are in the ratio 6 : 8 : 10. If the perimeter of the triangle is 288 cm, find the:
(i) longest side;
(ii) shortest side
(iii) difference between the longest and the shortest sides.

2. (a) An English textbook costs GHc 25.00. The author of the book agreed to take 20% of the cost of each book sold. If 1,702 copies were sold, calculate the author’s share.

(b) Simplify: 

(c)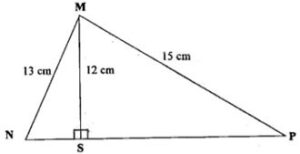 

In the diagram, |MN| = 13 cm, |MP| = 15 cm, |MS| = 12 cm and is perpendicular to NP. Calculate length of NP.

3. (a) Simplify leaving the answer in standard form.

(b) (i) Make r the subject of the relation:
(ii) From (b)(i), find the value of r when y = 3 and x = 10

(c) Juliet bought 1,756 kg of frozen chicken, 675 g of vegetables, and 95 g of corn oil from a shopping mall. What is the total weight of the items she bought in kilograms?

4. (a) The sum of the interior angles of a regular polygon is 900°. Find the number of sides of the polygon.

(b) Using a ruler and a pair of compasses only, construct:
(i) triangle XYZ such that the length XY = 10cm, angle XYZ = 30° and length YZ = 9 cm;
(ii) perpendicular from Z to meet line XY at P;
(iii) measures the:
(α) length PZ;
(β) angle XZY.
(iv) calculate, correct to the nearest whole number, the area of triangle XYZ.

5. (a) A property worth GHc 10,480.00 is shared between a widow and her 10 children in the ratio 1 : 4 respectively. The children shared their portions equally. Find each child’s share.

(b) The data shows the distribution of marks in a class test.

27  55  19  65  69  46
38  42  14  57  11  13
14  67  22  10  25  17
45  39  61  52  43  24
28  63  56  49  64  32

Use the data to answer the following questions:
(i) make a Stem and Leaf plot of the data;
(ii) how many students scored more than 10 marks and less than 20 marks?
(iii) what is the probability of a student scoring less than 20 marks?

6. (a) An aeroplane left the Kotoka International Airport on Wednesday at 7:26 pm and reached its destination after nine hours thirty minutes. Find the day and the time the aeroplane reached its destination.

(b)
(i) Using a scale of 2 cm to 2 units on both axes, draw two perpendicular axes Ox and Oy on a graph sheet for -10≤x≤10 and -12≤y≤12.
(ii) Draw on this graph, indicating the co-ordinates of all vertices, the quadrilateral ABCD with vertices A(0,10), B(-6,-2), C(-3,-11) and D(4,3)
(iii) Draw the line x = -2 to meet AB at P and CD at Q.
(iv) Measure angles BPQ and PQD
(v) State the relationship between:

(α) angles BPQ and PQD;
(β) lines AB and CD.

END OF PAPER 2 (ESSAY)

---

JUNE 2018
MATHEMATICS 2

ESSAY

SOLUTIONS

1. (a) Solve the inequality and represent the answer on the number line.

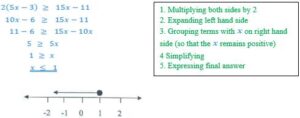
(b) Given that and , find 2t + k

(c) The sides of a triangle are in the ratio 6 : 8 : 10. If the perimeter of the triangle is 288 cm, find the:
(i) longest side;

(ii) shortest side

First Method

Second Method (using simple proportion)
If ratio     10 → 120 cm,
Then ratio 6 → ?   (less)
If less, more (10) divides

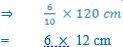
= 6 × 12 cm
= 72 cm

(iii) difference between the longest and the shortest sides.
Difference = Longest – Shortest
= 120 – 72
= 48 cm

2. (a) An English textbook costs GHc 25.00. The author of the book agreed to take 20% of the cost of each book sold. If 1,702 copies were sold, calculate the author’s share.

First Approach (finding his share for each book first)
Author’s share for each book = 20% of GHc 25.00
= 20% × 25.00

= 20/100  × 25
= GHc 5.00
Therefore Author’s share for 1,702 copies sold
= 1702 × 5 = 8510
= GHc 8510.00

Second Approach (finding the total sale first)
Total sales made from 1702 copies
= Total no. of copies × Selling price for each
= 1702 × 25
= GHc 42550
Therefore Author’s share for 1702
= 20% of GHC 42550

=
= 2 × 4255
= GHc 8510.00

(b) Simplify:

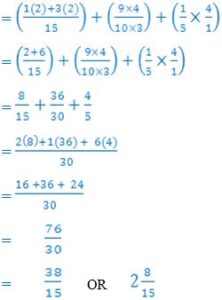
(c)

In the diagram, |MN| = 13 cm, |MP| = 15 cm, |MS| = 12 cm and MS is perpendicular to NP. Calculate length NP.

From the Pythagoras theorem, |NS|² + 12² = 13²
|NS|² = 13² – 12²
|NS|² = 169 – 144
|NS|² = 25
|NS| = √25
= 5 cm
Similarly, from the Pythagoras theorem,
|SP|² = 15² – 12²
         = 225 – 144
          = 81
|SP| =  √81
        = 9 cm

Hence, length NP = 5cm + 9cm
= 14cm

3. (a) Simplify , leaving the answer in standard form.

1st Method

=  21× 3
=  63
=  6.3 × 10   OR  6.3 × 10¹

2nd Method

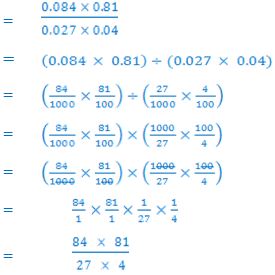
=        21× 3
=         63
=      6.3 × 10   OR  6.3 × 10¹

3rd Method

=        21× 3
=         63
=      6.3 × 10   OR  6.3 × 10¹

(b) (i) Make r the subject of the relation:

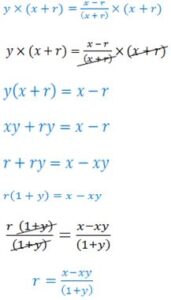
(ii) From (b)(i), find the value of r when y = 3 and x = 10

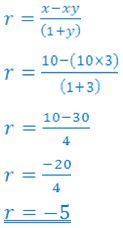
(c) Juliet bought 1,756 kg of frozen chicken, 675 g of vegetables, and 95 g of corn oil from a shopping mall. What is the total weight of the items she bought in kilograms?

Total weigh of items = 1,756 kg + 675 g + 95 g

First Approach (converting to g first)
1756 kg = 1756 × 1000 g = 1756000 g

Now adding in grams (g)

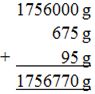
Converting to kg, we have = 1756.770 kg

Second Approach (converting to kg first)

675 g = = 0.675 kg
95 g = = 0.095 kg

Now adding in kilograms (kg)

 

4. (a) The sum of the interior angles of a regular polygon is 900°. Find the number of sides of the polygon.

Sum of interior angles = (n – 2) × 180° , where n = no. of sides
⇒        900° = 180°n – 360°
900° + 360° = 180°n
1260° = 180°n

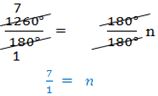
n = 7
Hence, the polygon has 7 sides

(b) Using a ruler and a pair of compasses only, construct:
(i) triangle XYZ such that the length XY = 10cm, angle XYZ = 30° and length YZ = 9 cm;
(ii) perpendicular from Z to meet line XY at P;

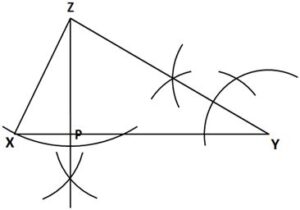
(iii) measure the:
(α) length = 4.5 cm or 4.4 cm or 4.6 cm
(β) angle = 86° or 85° or 87°

(iv) calculate, correct to the nearest whole number, the area of triangle XYZ.
Area of a triangle = 1/2 × Base × Height
Area of triangle XYZ = 1/2 × |XY| × |PZ|
= 1/2 × 10cm × 4.5
= 1/2 × 45
= 22.5
≈ 23 cm² (to nearest whole number)

Note: If 4.4 cm is used, Area = 22 cm
If 4.6 cm is used, Area = 23 cm

5. (a) A property worth GHc 10,480.00 is shared between a widow and her 10 children in the ratio 1 : 4 respectively. The children shared their portions equally. Find each child’s share.

1st Approach
The Children’s share =
=
= 8384
Each child’s share = = 838.4
= GHc 838.40

 

2nd Approach
The widow’s share =
=
= 2,096

The Children’s share = 10,480 – 2,096
= 8384

Each child’s share = = 838.4
= GHc 838.40

3rd Approach
The Children’s share = 4 × Widow’s share
= 4 × 2,096
= 8384
Each child’s share = = 838.4
= GHc 838.40

(b) The data shows the distribution of marks in a class test.

27 55 19 65 69 46
38 42 14 57 11 13
14 67 22 10 25 17
45 39 61 52 43 24
28 63 56 49 64 32

Use the data to answer the following questions:
(i) make a Stem and Leaf plot of the data;

Stem Leaf
1 0, 1, 3, 4, 4, 7, 9
2 2, 4, 5, 7, 8,
3 2, 8, 9
4 2, 3, 5, 6, 9
5 2, 5, 6, 7,
6 1, 3, 4, 5, 7, 9

(ii) how many students scored more than 10 marks and less than 20 marks?
= 6 students

(iii) what is the probability of a student scoring less than 20 marks?
Probability =
=

6. (a) An aeroplane left the Kotoka International Airport on Wednesday at 7:26 pm and reached its destination after nine hours thirty minutes. Find the day and the time the aeroplane reached its destination.

1st approach
Departure time = 7:26 pm;
Duration of flight = 9 h 30 min

 

2nd approach

7:26 pm = 7:26 + 12:00 = 19:26 GMT

The aeroplane arrives on Thursday at 4:56 am.

(b)
(i) Using a scale of 2 cm to 2 units on both axes, draw two perpendicular axes Ox and Oy on a graph sheet for and .
(ii) Draw on this graph, indicating the co-ordinates of all vertices, the quadrilateral ABCD with vertices and
(iii) Draw the line to meet AB at P and CD at Q.

(iv) Measure angles BPQ and PQD
Angle BPQ = 26° or 25° or 27°
Angle PQD = 26° or 25° or 27°

(i) State the relationship between:
(α) angles BPQ and PQD;
They are alternate angles

(β) lines AB and CD.
They are parallel