
BECE Mathematics 2016 Past Questions & Answers – Paper 2 (Written/Essay)
JUNE 2016
MATHEMATICS 2
PAPER 2
ESSAY
1 HOUR
Answer four questions only.
All questions carry equal marks.
All working must be clearly shown.
Marks will not be awarded for correct answers without corresponding working
1. (a) In an examination, 50 candidates sat for either Mathematics or English Language. 60% passed in Mathematics and 48% passed in English Language. If each candidate passed in at least one of the subjects, how many candidates passed in :
(i) Mathematics?
(ii) English Language?
(b) Illustrate the information given in (a) on a Venn diagram.
(c) Using the Venn diagram, find the number of candidates who passed in
(i) both subjects;
(ii) Mathematics only.
(d) If ![]() are equal vectors, find the values of x and y
are equal vectors, find the values of x and y
2. (a) The cost (P), in Ghana cedis, of producing n items is given by the formula ![]()
. Find the:
(i) cost of producing 2,000 items;
(ii) number of items that will be produced with GHC 2,400.00;
(iii) cost when no items are produced.
(b) A passenger travelling by air is allowed a maximum of 20 kg luggage.
A man has four bags weighing 3.5 kg, 15 kg, 2 kg and 1.5 kg.
(i) Find the excess weight of his luggage
(ii) Express the excess weight as a percentage of the maximum weight allowed.
3. (a) A doctor treated 2,000 patients over a period of time. If he worked for 5 hours a day and spent 15 minutes on each patient, how many days did the doctor spend to treat all the patients?
(b) The pie chart shows the distribution of textbooks to six classes A, B, C, D, E and F in a school.
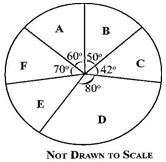
(i) If Class D was given 720 textbooks, how many textbooks were distributed to each of the remaining classes?
(ii) What is the average number of textbooks distributed to the classes?
(iii) How many classes had less than the average number of textbooks distributed?
4. (a) Using a scale of 2 cm to 1 unit on both axes, draw on a graph sheet, two perpendicular axes OX and OY for –5≤x≤5 and -5≤y≤5
(i) Plot, indicating the coordinates of all points P(1, 1), Q(1, 2), R(2, 2) and S(2, 1) on a graph sheet. Join the points to form square PQRS.
(ii) Draw and indicate clearly all coordinates, the image P1Q1R1S1 of square PQRS under an enlargement from the origin with a scale factor of 2, where P → P1, Q→Q1, R→R1 and S→S1.
(iii) Draw and indicate clearly all coordinates, the image P2Q2R2S2 of square P1Q1R1S1 under a reflection in the x-axis where P1→P2, Q1→Q2, R1→R2 and S1→S2
(b) Using the graph in 4(a), find the gradient of line R2S.
5. (a) Given that u = 4, t = 5, a = 10 and s=ut+½at2 , find the value of s.
(b) The selling price of a gas cooker is GHC450.00. If a customer is allowed a discount of 20%, calculate the :
(i) discount;
(ii) amount paid by the customer.
(c) A crate of minerals containing ten bottles of Coca Cola and fourteen bottles of Fanta was given to some children for a birthday party. If a child chose a drink at random from the crate, find the probability that it was Fanta.
6. (a) Using a ruler and a pair of compasses only, construct:
(i) triangle XYZ with |XY| = 9 cm, |YZ| = 12 cm and |XZ| = 8cm;
(ii) the perpendicular bisector of line XY;
(iii) the perpendicular bisector of line XZ.
(b) (i) Label the point of intersection of the two bisectors as T;
(ii) With point T as centre, draw a circle of radius 6 cm.
(c) Measure:
(i) |TX|
(ii) angle XYZ
END OF PAPER 2 (Essay)
JUNE 2016
MATHEMATICS 2
ESSAY
SOLUTIONS
1. (a) (i) Number of candidates who passed in Mathematics
= 60% of 50 candidates
= ![]()
= 6 x 5
= 30
(ii) Number of candidates who passed in English Language
= 48% of 50 candidates
= ![]()
= 24
(b) Venn diagram
Let U = Total number of Candidates,
M = Number of candidates who passed in Mathematics and
E = Number of candidates who passed in English
b = Number of candidates who passed in both Mathematics and English
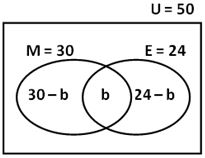
(c) (i) From the Venn diagram above,
30 – b + b + 24 – b = 50
⇒ 54 – b = 50
⇒ b = 4
Hence, 4 candidates passed in both subjects
(ii) Mathematics only = 30 – b
= 30 – 4
= 26
(d) If a = b, then
taking the horizontal component, 4 = 2x
⇒ x = 4 ÷ 2
⇒ x = 2
Now, taking the vertical component, – 5 = 3 + y
⇒ y = – 5 – 3
⇒ y = – 8
2. (a) (i) Since Cost, ![]() where n = the number of items,
where n = the number of items,
Cost of producing 2,000 items
= 
Cost of producing 2,000 items = GHC 3,300.00
(ii) Method 1 (Substitution and solving)

n = 800
Hence, the number of items = 800
(ii) Method 2 (Making n the subject, substituting and simplifying)

n = 800
Hence, the number of items = 800
(iii) When no items are produced, n = 0

Cost when no items are produced = GHC 1,800.00
(b) (i) Total weight of four bags
= 3.5 + 15 + 2 + 1.5
= 22 kg
Hence, excess weight = 22 – 20
= 2 kg
(ii) Excess weight as a percentage of maximum weight allowed
= ![]()
= 2 x 5%
= 10%
3. (a) If doctor works 5 hours a day and spends 15 minutes on each patient, then
Number of patients treated a day
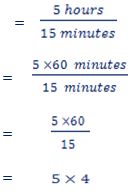
= 20
Hence, he treats 20 patients each day
Number of days used
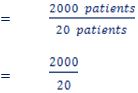
= 100
Hence, he treats 2000 patients in 100 days
NOTE: Alternatively the idea of ratio or simple proportion can be applied to solve the question.
(b) (i)
If Class D: (80°) → 720 textbooks
Then Class A: (60°) → ? (less)
If less, then more (80°) divides
⇒ ![]()
= 60 × 9
= 540 textbooks
Now, if number of textbooks of Class A (60°) = 60 × 9,
then, Class B (50°) = 50 × 9 = 450 textbooks
Class C (42°) = 42 × 9 = 378 textbooks
Class F (70°) = 70 × 9 = 630 textbooks
Now, angle for Class E = 360° – (70°+60°+50°+42°+80°)
= 360°– 302°
= 58°
Hence, Class E (58°) = 58 × 9
= 522 textbooks
(ii) Average number of textbooks =
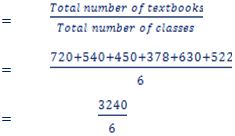
= 540 textbooks
(iii) Number of classes which had less than average
(Classes B, C and E had less than 540 textbooks)
= 3 classes
4. (a)
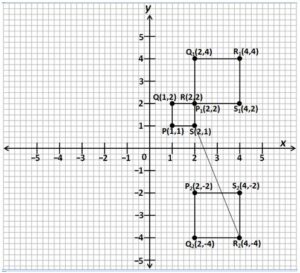
(b) Gradient of line R2S

= – 2.5 or 2½
5. (a) From
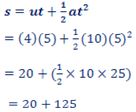
Hence s = 145
(b) (i) Discount = 20% of GHC 450.00
= ![]()
= 2 × 45
Discount = GHC 90
(ii) Method 1
Amount paid = Original Selling Price – Discount
= 450 – 90
= GHC 360
Method 2
Amount paid = 80% of GHC 450.00 [100% – 20% = 80%]
= ![]()
= 8 × 45
= 360
The amount paid by the customer = GHC 360.00
(c) Probability of randomly choosing Fanta

6. (a), (b)
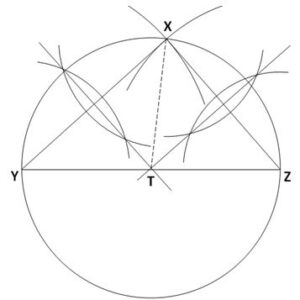
(c) (i) |TX| = 6 cm (± 0.1cm)
(ii) angle XYZ = 40° (±1°)
END OF PAPER 2 (Essay) SOLUTIONS
This Post Has 0 Comments