BECE 2014 Mathematics Past Questions Paper 2 (Essay)

JUNE 2014
MATHEMATICS 2

Essay
1 hour

1.(a) P = {factors of 30}
Q = {Multiples of 5 less than 40}
Find P ∩ Q

(b) A trader saved GH¢ 200.00 for 3 years at 12% simple interest per annum.
What will be the total amount in the trader’s account at the end of the 3 years?

(c) Evaluate and leave your answer in standard form.

2. (a) (i) Ama scored 82, 74 and 90 in three tests. What mark should she score in the fourth test so that her average mark for the four tests would be 85?

(ii) What was her median score in the four tests?

b)

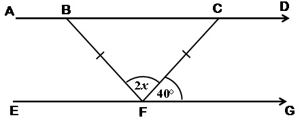
In the diagram    angle CFG = 40° and triangle BCF is isosceles.
Find the value of :
(i)   angle CBF
(ii)   angle DCF;
(iii)   x

3. (a) Solve for x, if 

(b) The following shows the distribution of marks of students in an examination.

(i) Make a stem-and-leaf plot of the marks above
(ii) Find the probability of selecting a student who scored between 40 and 50.
(iii) Find the number of students who passed the examination, if the pass mark was 30.

4. (a) A box has length 8.0 cm, width 5.0 cm and height 10.0 cm.
Find the:
(i) total surface area of the box
(ii) the volume of the box.

(b) (i) Using a scale of 2cm to 1 unit on both axes, draw two perpendicular axes Ox and Oy on a graph sheet.
(ii) On the same graph sheet mark the x-axis from –5 to 5 and the y-axis from – 6 to 6.
(iii) Plot and join the points
A(0, 3), B(2, 3), C(4, 5) to form triangle ABC.
(iv) Draw the image A1B1C1 of triangle ABC under a translation by the vector 

(v) Draw the image A2B2C2 of triangle ABC under a reflection in the x – axis.

5. (a) Using a ruler and a pair of compass only;
(i) construct triangle PQR such that 

(ii) construct the perpendicular bisector of 

(iii) construct the perpendicular bisector of 

(iv) Label the point of intersection of

(v) With N as centre and radius equal to |PN|, draw a circle.

(b) (i) Measure the radius of the circle.
(ii) Calculate the circumference of the circle, correct to 3 significant figures.

6. (a) Factorize completely 6xy – 3y + 4x – 2

(b)

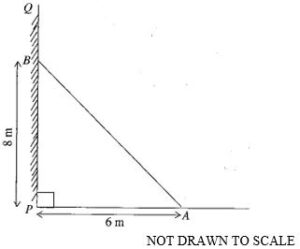
The diagram shows a ladder AB which leans against a vertical wall PQ at B.
If |PB| is 8 m, and the other end of the ladder is 6 m away from the foot of the wall (at P), find the length of the ladder (|AB|)

(c) Kojo had 1800 bags of rice in stock for sale. In January, he sold ⅔ of it.
In February, he sold ¾ of what was left.

(i) What fraction of the stock of rice did he sell
(α) in February?
(β) in January and February?

(ii) How many bags of rice were left unsold, by the end of February?

END OF PAPER 2